Nelson Rules
Nelson rules are a method in process control of determining if some measured variable is out of control (unpredictable versus consistent). Rules, for detecting "out-of-control" or non-random conditions were first postulated by Walter A. Shewhart [1] in the 1920s. The Nelson rules were first published in the October 1984 issue of the Journal of Quality Technology in an article by Lloyd S Nelson.[2]
The rules are applied to a control chart on which the magnitude of some variable is plotted against time. The rules are based on the mean value and the standard deviationof the samples.
| Rule | Description | Chart Example | Problem Indicated |
|---|---|---|---|
| One point is more than 3 standard deviations from the mean. |  |
One sample (two shown in this case) is grossly out of control. | |
| Nine (or more) points in a row are on the same side of the mean. | 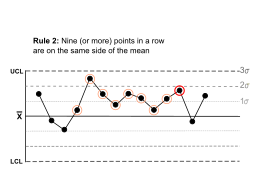 |
Some prolonged bias exists. | |
| Six (or more) points in a row are continually increasing (or decreasing). |  |
A trend exists. | |
| Fourteen (or more) points in a row alternate in direction, increasing then decreasing. | 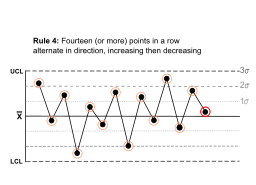 |
This much oscillation is beyond noise.Note that the rule is concerned with directionality only. The position of the mean and the size of the standard deviation have no bearing. | |
| Two (or three) out of three points in a row are more than 2 standard deviations from the mean in the same direction. |  |
There is a medium tendency for samples to be mediumly out of control.The side of the mean for the third point is unspecified. | |
| Four (or five) out of five points in a row are more than 1 standard deviation from the mean in the same direction. | 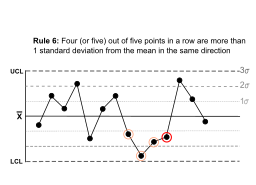 |
There is a strong tendency for samples to be slightly out of control.The side of the mean for the fifth point is unspecified. | |
| Fifteen points in a row are all within 1 standard deviation of the mean on either side of the mean. | 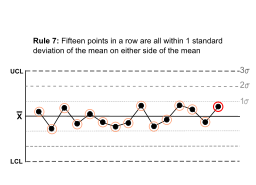 |
With 1 standard deviation, greater variation would be expected. | |
| Eight points in a row exist with none within 1 standard deviation of the mean and the points are in both directions from the mean. | 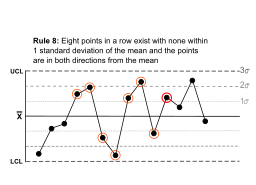 |
Jumping from above to below whilst missing the first standard deviation band is rarely random. |
The above eight rules apply to a chart of a variable value.
'통계적 공정 관리 (SPC) > 통계.품질.6Sigma' 카테고리의 다른 글
| 3시그마 규칙 ( 68-95-99.7 규칙 ) (0) | 2020.02.20 |
|---|---|
| 공정능력 PP, PPK, 장기, 단기 (2) | 2019.06.03 |
| 공정능력 CP, CPK, 시그마수준 (10) | 2019.06.03 |
| 계수형 관리도의 정의 (1) | 2016.07.18 |
| 평균 그리고 표준편차의 개념 (4) | 2016.01.07 |



